К списку статей

Распространение н. и. Н. и. может распространяться вдоль волокна без затухания и с пост. скоростью. Это связано с тем, что необходимая для передачи сигнала энергия не поступает из единого центра, а черпается на месте, в каждой точке волокна. В соответствии с двумя типами волокон существуют два способа передачи н. и.: непрерывный и сальтаторный (скачкообразный), когда импульс движется от одного перехвата Ранвье к другому, перепрыгивая через области миелиновой изоляции.

В случае немиелинизир. волокна распределение мембранного потенциала j(x, t)определяется ур-нием:

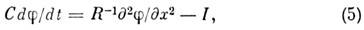
где С - ёмкость мембраны, приходящаяся на единицу длины волокна, R - сумма продольных (внутриклеточного и внеклеточного) сопротивлений на единицу длины волокна, I - ионный ток, протекающий через мембрану волокна единичной длины. Электрич. ток I является функционалом от потенциала j, к-рый зависит от времени t и координаты х. Эта зависимость определяется ур-ниями (2) -(4).

Вид функционала I специфичен для биологически возбудимой среды. Однако ур-ние (5), если отвлечься от вида I, имеет более общий характер и описывает многие физ. явления, напр. процесс горения. Поэтому передачу Н. и. уподобляют горению порохового шнура. Если в бегущем пламени процесс поджигания осуществляется за счёт теплопроводности, то в Н. и. возбуждение происходит при помощи т. н. локальных токов (рис. 5).

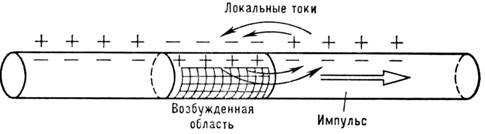
Рис. 5. Локальные токи, обеспечивающие распространение нервного импульса.

Ур-ния Ходжкина - Хаксли для распространения Н. и. решались численно. Полученные решения вместе с накопленными эксперим. данными показали, что распространение н. и. не зависит от деталей процесса возбуждения. Качеств. картину распространения н. и. можно получить при помощи простых моделей, отражающих лишь общие свойства возбуждения. Такой подход позволил рассчитывать скорость и форму н. и. в однородном волокне, их изменение при наличии неоднород-ностей и даже сложные режимы распространения возбуждения в активных средах, напр. в сердечной мышце. Существует неск. матем. моделей подобного рода. Простейшая из них такова. Ионный ток, протекающий через мембрану при прохождении н. и., является знакопеременным: вначале он течёт внутрь волокна, а потом наружу. Поэтому его можно аппроксимировать кусочно-постоянной функцией (рис. 2, г). Возбуждение происходит, когда мембранный потенциал сдвигается на пороговую величину j*. В этот момент возникает ток, направленный внутрь волокна и равный по модулю j'. Спустя время t' ток меняется на противоположный, равный j''. Эта фаза продолжается в течение времени ~ t''. Автомодельное решение ур-ния (5) можно найти как функцию переменной t = х/u, где u - скорость распространения н. и. (рис. 2, б).

В реальных волокнах время t' достаточно велико, поэтому только оно определяет скорость u, для к-рой справедлива ф-ла: 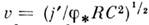. Учитывая, что j' ~ ~d, R ~ d² и С ~ d, где d - диаметр волокна, находим в согласии с экспериментом, что u ~ d^1/2. С помощью кусочно-постоянной аппроксимации находят форму потенциала действия.

Ур-ние (5) для распространяющегося н. и. в действительности допускает два решения. Второе решение оказывается неустойчивым; оно даёт н. и. со значительно меньшей скоростью и амплитудой потенциала. Наличие второго, неустойчивого, решения имеет аналогию в теории горения. При распространении пламени с боковым теплоотводом также возможно возникновение неустойчивого режима. Простую аналитич. модель н. и. можно усовершенствовать, учитывая дополнит. детали.

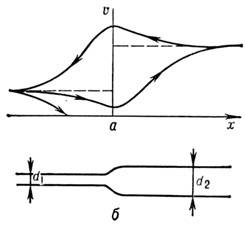
При изменении сечения и при ветвлении нервных волокон прохождение н. и. может быть затруднено или даже полностью блокировано. В расширяющемся волокне (рис. 6) скорость импульса по мере приближения к расширению убывает, а после расширения начинает расти, пока не выйдет на новое стационарное значение. Замедление н. и. тем сильнее, чем больше разница в сечениях. При достаточно большом расширении н. и. останавливается. Существует критич. расширение волокна, к-рое задерживает н. и.

При обратном движении н. и. (из широкого волокна в узкое) блокирования не происходит, но изменение скорости носит противоположный характер. При подходе к сужению скорость н. и. увеличивается, а затем начинает спадать до нового стационарного значения. На графике скорости (рис., 6а) получается своего рода петля гистерезиса.

Рие. 6. Прохождение нервных импульсов по расширяющемуся волокну: а - изменение скорости импульса в зависимости от его направления; б -схематическое изображение расширяющегося волокна.

Другой тип неоднородности - ветвление волокон. В узле ветвления возможны разл. варианты прохождения и блокирования импульсов. При несинхронном подходе н. и. условие блокирования зависит от временного сдвига. Если временной сдвиг между импульсами мал, то они помогают друг другу проникнуть в широкое третье волокно. Если сдвиг достаточно велик, то нервные импульсы мешают друг другу. Связано это с тем, что н. и., подошедший первым, но не сумевший возбудить третье волокно, частично переводит узел в рефракторное состояние. Кроме того, возникает эффект синхронизации: по мере приближения н. и. к узлу их запаздывание друг относительно друга уменьшается.

Источник